Natural frequency is the vibration inherent to an object and is particularly important in machinery to avoid resonance. The eigenfrequency analysis (or eigenvalue analysis) is used to obtain the eigenfrequency, and the eigenfrequency (eigenvalue) and mode shape are output as analysis results. The mode shape represents how structures shake (deformation shape) when they vibrate, and it’s evaluated as a set with the eigenfrequency.
One of the frequent issues is the requirement to increase natural frequency. The main purpose of it is to avoid resonance phenomena, but the avoidance is thought to result in increased strength of the structure. However, raising natural frequency is often difficult under limited design conditions.
Natural frequency of a spring-mass system with the simplest single degree of freedom is given by the following equation.
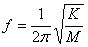・・・(1)
f:natural frequency [Hz]
M:mass [kg]
K:spring constant [N/m]
This formula is very simple, but very useful for design purposes. Considering this equation, we can see that the only way to increase the natural frequency is to decrease M or increase K. Now, let’s consider them in order.
M: Reduction in mass
At the beginning, we consider a simple but easily forgotten method of reducing M, i.e., mass, when raising natural frequency. The point is simply that if you reduce the mass, natural frequency will increase. For example, suppose there is a component weighing 10 kg with a natural frequency of 10 Hz. When its weight is reduced by 10% to 9kg, then 10Hz×√(10/9)=10.5Hz., and that means natural frequency increases by 5%. However, it is important to note that the above is only a case where the total mass affects natural frequency, such as when the mass is attached to the tip of a spring. As a matter of fact, mass is distributed and the effect depends on the shape of the object. When only one part of a structure vibrates, reducing the weight of the part will cause the effect above, but when the entire structure shakes, the effect will be less. In such cases, the mode shapes obtained as a result of natural vibration analysis are important information for understanding where the vibration occurs.
Another point to note is that reducing the weight by reducing cross-sectional area or the thickness of plates, etc. may cause a reduction in stiffness. In other words, weight reduction is useless if the reduction in mass is offset by a decrease in rigidity (K). And it is necessary to keep in mind that such reduction of weight is not good from the strength point of view either.
Despite the above caveats, “weight reduction” is a very desirable measure for increase natural frequencies because it reduces the amount of material used, and in many cases, machines are required to be lighter.
K: Increase in stiffness
This is the simplest case, though there are some caveats. When ferrous materials such as carbon steel, SUS, etc., are used, the alternative material will be required a higher modulus of longitudinal elasticity than the ferrous one, and that is hardly found. When aluminum is used as a material, options such as using iron-based materials will be available. It should be noted, however, that using iron instead of aluminum increases the density by 2.8 times, resulting in a significant increase in mass.
Using carbon fiber reinforced plastic (CFRP) may reduce mass and improve stiffness in the cases above.
Increase stiffness of materials
This is the easiest method to do, but if you are using ferrous materials (carbon steel, SUS, etc.), you will need a material with a higher modulus of longitudinal elasticity, making it more difficult. If aluminum is used, there are options such as using iron-based materials, but on the other hand, it is important to note that if you use iron instead of aluminum, the density will be 2.8 times higher and the mass will increase significantly.
In such cases, using carbon fiber reinforced plastic (CFRP) may reduce mass and improve rigidity.
Increase the rigidity of member
In simple cases, increasing the cross-sectional area of the member or increasing the thickness of the plate can be considered. For example, the natural frequency of a cantilever beam is related to the second moment of area. Therefore, increasing the second moment of area will also increase the natural frequency.
Additionally, the out-of-plane mode of a flat plate can be improved by adding ribs to the flat plate. This is equivalent to partially increasing plate thickness.
Restraints of vibrating parts
In the simplest case, changing a cantilevered beam to a double-sided beam will dramatically increase natural frequency. However, actual structures have design constraints, so it is not that easy. if you carefully check the mode shape and find out where the deviation is, you may be able to take countermeasures. The basic countermeasure is to check the mode shape carefully and restrain the anti-node (where the mode deformation is large). Conversely and just to be sure, you cannot expect to improve natural frequency if you constrain the nodes of the mode.